Quantum computing threat: How to prepare for a smooth transition to post-quantum cryptography

Cryptography is a critical component in all connected devices. While its usage often goes unnoticed, it is the fundamental building block of many security solutions. Use cases, such as Over-the-Air (OtA) updates, secure flashing, car-to-car communication, and remote maintenance, rely on cryptography to protect our customers’ data and our products against increasingly sophisticated cyberattacks. Security in all of these use cases depends on well-known public-key algorithms. In turn, these algorithms depend on the difficulty of the following mathematical problems: integer factorization and elliptic-curve discrete logarithm.

With powerful quantum computers on the horizon, however, the field of cryptography is on the brink of a major overhaul. Since quantum computers operate on principles of quantum mechanics, e.g., superposition and entanglement, they are capable of efficiently solving complex mathematical problems that are intractable on traditional computers. Their tremendous computing power will eventually allow them to break nearly all modern cryptographic primitives. Yet, their field of application is not limited to cryptography. In fact, their impact on use cases, such as analyzing data sets via means of artificial intelligence, modeling complex chemical structures for drug development, and solving optimization problems for the transport and finance industry, is expected to be tremendous.

The quantum threat, however, has sparked increased interest in the field of post-quantum cryptography (PQC), i.e., cryptographic algorithms that withstand attacks from quantum computers by relying on alternative mathematical problems. While such powerful quantum computers do not exist yet, the advent of “cryptographically-relevant” quantum computers seems inevitable, especially in light of recent landmark achievements by various leading tech companies.

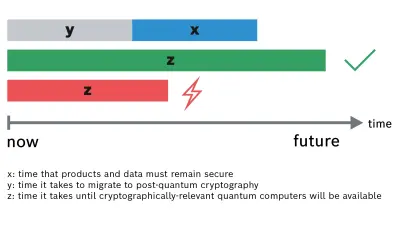
In order to assess the threat quantum computers pose to systems, products, or applications, one can refer to Michele Mosca’s theorem (see Figure 1): Typically, data needs to be secure for at least x years depending on the sensitivity of the data. If it takes y years to migrate to post-quantum cryptography and if cryptographically-relevant quantum computers will not be available for another z years, y+x must be smaller than z. Otherwise, it is already too late because cryptographically-relevant quantum computers will become reality before the migration to PQC has finished, resulting in insecure systems, products, or applications.

Knowing that the transition to new cryptographic primitives is usually a slow and burdensome process makes the threat posed by quantum computers a very real and urgent matter – especially for mobility solutions and industrial technologies.

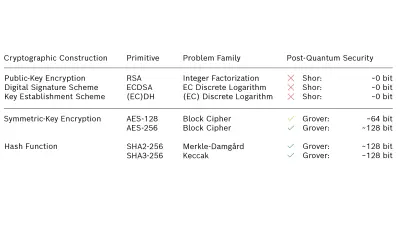
Developments in the field of quantum computing have shown that there is an increasing need for revising the algorithms used for digital signatures and key establishment, while symmetric block algorithms are still considered secure.

In 1997, Shor developed an algorithm that solves the integer factorization and discrete logarithm problem in polynomial time on a large-enough quantum computer. Since not only the Rivest–Shamir–Adleman (RSA) cryptosystem relies on this complexity assumption, but also signature schemes based on elliptic-curve cryptography (ECC) as well as Diffie-Hellman (DH) key establishment and its elliptic curve (EC) variants, all public-key cryptosystems in widespread use today will be broken by Shor’s quantum algorithm.

Grover’s search algorithm is another quantum algorithm that affects symmetric block algorithms, e.g., AES, as well as hash functions, e.g., the family of secure hash algorithms (SHA). It lowers the classical complexity of searching an unstructured list of size n by a factor of √n resulting in a quadratic speedup. However, the impact of Grover’s search algorithm is expected to be less critical because doubling the size of the symmetric key or the size of the hash function mitigates its speedup.

Since it takes a long time to develop and refine a new generation of cryptographic algorithms, there are already several standardization efforts under way to tackle this problem. Most notably, the National Institute of Standards and Technology (NIST) started its Post-Quantum Cryptography Standardization in 2016. Its standardization process is conducted in the form of an “open competition”: The international research community is invited to submit, vet, and improve submissions from all major PQC families. In the initial round, almost 80 PQC schemes had already been submitted.

As part of the NIST competition, different algorithms will be chosen for digital signatures and key establishment. As recently as July 2020, this competition entered its third round, which includes seven “finalist” algorithms that will be considered for standardization in the next two years, and eight “alternate” algorithms, which may be standardized after an additional round of study.

NIST will announce its final selection within the next few months. The respective draft standards are then expected to be available for public comment between 2022 and 2023. Eventually, a finalized standard consisting of two to three post-quantum algorithms for key exchange and digital signatures will be available at the latest by 2024.

The post-quantum algorithms submitted to the NIST competition fall into five categories, according to the problem family they are based on:

• Code-Based: The security of such systems is based on the difficulty of inverting a random linear code.
• Lattice-Based: The security of such systems relies on the shortest vector problem and learning with errors problem.
• Isogeny-Based: The security of such systems is based on the difficult mathematical problem of finding isogenies between special elliptic curves.
• Multivariate-Equations-Based: The security of these systems is based on the fact that solving multivariate quadratic systems of equations over finite fields is NP-hard.
• Hash-Based Signatures: The security of these systems relies only on the security of the underlying hash function.

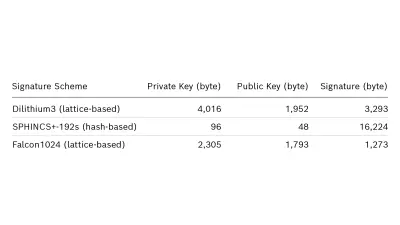
Compared to current public-key cryptosystems, PQC primitives generally incur a higher cost in some metric: computational cost, storage requirements, or network bandwidth. As a consequence, the impact of these novel schemes needs to be carefully evaluated when integrated into devices, protocols, and applications. For example, many of the proposed schemes produce very large signatures or require very large key pairs. As a result, some of them may not be suitable for resource-constrained electronic control units (ECUs) or deeply-embedded sensors, which possess only a limited amount of secure memory and computational resources. Especially for use cases with strict real-time requirements, e.g., car-to-car communication or critical control messages, the selection of post-quantum algorithms is a challenge.

See Table 2 for key sizes of three different algorithms that are considered in the third round of the NIST PQC standardization process.

But even after post-quantum schemes have ben standardized, several issues need to be considered before they can be deployed on a large-scale:

• Applications should be designed with cryptographic agility in mind. This will allow cryptographic parameters and schemes to be replaced dynamically while the underlying application remains fully functional. In turn, this requires remote software updates to be in place and the use of standardized cryptographic interfaces. As a result, cryptographic agility will become a desirable feature in many applications.
• Performance restrictions need to be addressed by either taking advantage of existing hardware acceleration solutions or by developing entirely new hardware security solutions.
• Relevant protocols need to be redesigned to include post-quantum cryptography. For example, to overcome inherent limitations when transferring larger post-quantum cryptographic keys and certificates.
  In one of our previous works, we focused on the industrial communication standard Open Platform Communications Unified Architecture (OPC UA). In this work, we proposed two novel solutions for the integration of post-quantum primitives (digital signatures and key establishment) into OPC UA: a hybrid solution combining conventional cryptography with PQC and a solution solely based on PQC. Our hybrid solution provides post-quantum security for early adopters but comes with additional performance and communication requirements. Since they are already widely studied, hybrid constructions for key exchange and signatures are considered a feasible transitional strategy that protects today’s communication against tomorrow’s attacks aided by quantum computers, e.g., “harvest now, decrypt later” attacks.
  Our solution solely based on PQC shows superior performance across all evaluated security levels in terms of handshake duration compared to conventional OPC UA, but comes at the cost of increased sizes for handshake messages.
  For more technical details see our paper: Towards Post-Quantum Security for Cyber-Physical Systems: Integrating PQC into Industrial M2M Communication
• Finally, a smooth transition from current cryptography to post-quantum cryptography needs to be ensured. For example, special care needs to be taken to ensure a smooth transition to post-quantum public-key infrastructures (PKIs). To tackle this problem, we proposed a novel two-step migration strategy based on the concept of mixed certificate chains for the TLS network protocol. A first intermediate step combines trusted hash-based signature schemes at the root level of a PKI with the conventional signature scheme ECDSA at the other PKI levels to prepare for a seamless transition to PQC-based authentication. The final migration step eventually aims for complete post-quantum security, where we evaluated the combination of hash-based signature schemes at the root level with lattice-based schemes at the intermediate and end entity level. Our results show that mixed certificate chains containing hash-based signature schemes only at the root certificate authority (CA) level led to feasible connection establishment times despite the increase in communication size.
  For more technical details see our recent paper: Mixed Certificate Chains for the Transition to Post-Quantum Authentication in TLS 1.3